As funções devem ser caracterizadas de acordo com algumas condições de existência:
Dois conjuntos: um denominado domínio e outro contradomínio.
Uma expressão y = f(x) associando os valores de x e y, formando pares ordenados pertencentes aos conjuntos domínio e contradomínio.
Através de alguns exemplos demonstraremos como determinar o domínio de uma função, isto é, descobrir quais os números que a função não pode assumir para que a sua condição de existência não seja afetada.
a)

Nesse caso o denominador não pode ser nulo, pois não existe divisão por zero na Matemática.
x – 1 ≠ 0
x ≠ 1
Portanto, D(f) = {x Є R / x ≠ 1} = R – {1}.
b)

Nos números reais, o radicando de uma raiz de índice não pode ser negativo.
4x – 6 ≥ 0
4x 6
x ≥ 6/4
x ≥ 3/2
Portanto, D(f) = {x Є R / x ≥ 3/2}
c)

O radicando de uma raiz de índice ímpar pode ser um número negativo, nulo ou positivo, isto é, 3x – 9 pode assumir qualquer valor real. Portanto, D(f) = R.
d)

Nesse caso temos restrições tanto no numerador quanto no denominador. As restrições podem ser calculadas da seguinte maneira:
I) 2 – x ≥ 0 → – x ≥ – 2 → x ≤ 2
II) x + 1 > 0 → x > – 1
Executando a intersecção entre I e II, obtemos:

Portanto, D(f) = {x Є R / –1 < x ≤ 2} → ] –1, 2]. Dois conjuntos: um denominado domínio e outro contradomínio.
Uma expressão y = f(x) associando os valores de x e y, formando pares ordenados pertencentes aos conjuntos domínio e contradomínio.
Através de alguns exemplos demonstraremos como determinar o domínio de uma função, isto é, descobrir quais os números que a função não pode assumir para que a sua condição de existência não seja afetada.
a)

Nesse caso o denominador não pode ser nulo, pois não existe divisão por zero na Matemática.
x – 1 ≠ 0
x ≠ 1
Portanto, D(f) = {x Є R / x ≠ 1} = R – {1}.
b)
Nos números reais, o radicando de uma raiz de índice não pode ser negativo.
4x – 6 ≥ 0
4x 6
x ≥ 6/4
x ≥ 3/2
Portanto, D(f) = {x Є R / x ≥ 3/2}
c)
O radicando de uma raiz de índice ímpar pode ser um número negativo, nulo ou positivo, isto é, 3x – 9 pode assumir qualquer valor real. Portanto, D(f) = R.
d)

Nesse caso temos restrições tanto no numerador quanto no denominador. As restrições podem ser calculadas da seguinte maneira:
I) 2 – x ≥ 0 → – x ≥ – 2 → x ≤ 2
II) x + 1 > 0 → x > – 1
Executando a intersecção entre I e II, obtemos:

É importante estar atento a determinadas situações envolvendo funções, o conhecimento e a habilidade em lidar com tais condições é consequência de muito estudo e dedicação por parte dos estudantes. Tais condições de existência das funções são cobradas em questões de vestibulares de diversas universidades brasileiras, em virtude de o conteúdo possuir inúmeras aplicações no cotidiano.
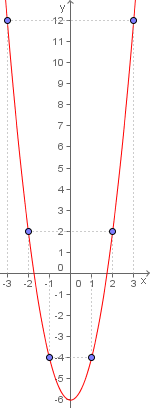 Vamos analisar a função
Vamos analisar a função 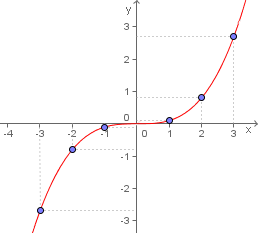 Vamos analisar a função
Vamos analisar a função 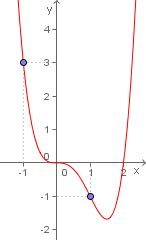 Como podemos observar, não existe a simetria visual vistas nos gráficos anteriores, nem quanto a uma função par, nem quanto a uma função ímpar.
Como podemos observar, não existe a simetria visual vistas nos gráficos anteriores, nem quanto a uma função par, nem quanto a uma função ímpar.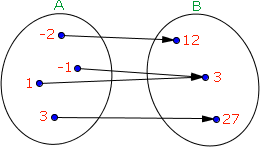 Vamos analisar o
Vamos analisar o  Vejamos agora este outro
Vejamos agora este outro  Na explicação do último tipo de função vamos analisar este outro
Na explicação do último tipo de função vamos analisar este outro  Para iniciarmos o estudo das
Para iniciarmos o estudo das