A Geometria Analítica é uma parte da Matemática , que através de processos particulares , estabelece as relações existentes entre a Álgebra e a Geometria. Desse modo , uma reta , uma circunferência ou uma figura podem ter suas propriedades estudadas através de métodos algébricos .
Os estudos iniciais da Geometria Analítica se deram no século XVII , e devem-se ao filósofo e matemático francês René Descartes (1596 - 1650), inventor das coordenadas cartesianas (assim chamadas em sua homenagem), que permitiram a representação numérica de propriedades geométricas. No seu livro Discurso sobre o Método, escrito em 1637, aparece a célebre frase em latim "Cogito ergo sum" , ou seja: "Penso, logo existo".
1.1 - Coordenadas cartesianas na reta
Seja a reta r na Fig. abaixo e sobre ela tomemos um ponto O chamado origem.
Adotemos uma unidade de medida e suponhamos que os comprimentos medidos a partir de O, sejam positivos à direita e negativos à esquerda.
O comprimento do segmento OA é igual a 1 u.c (u.c = unidade de comprimento). É fácil concluir que existe uma correspondência um a um (correspondência biunívoca) entre o conjunto dos pontos da reta e o conjunto R dos números reais. Os números são chamados abscissas dos pontos. Assim, a abscissa do ponto A’ é -1, a abscissa da origem O é 0, a abscissa do ponto A
é 1, etc.
A reta r é chamada eixo das abscissas.
1.2 - Coordenadas cartesianas no plano
Com o modo simples de se representar números numa reta, visto acima, podemos estender a idéia para o plano, basta que para isto consideremos duas retas perpendiculares que se interceptem num ponto O, que será a origem do sistema. Veja a Fig. a seguir:
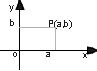
Dizemos que a é a abscissa do ponto P e b é a ordenada do ponto P.
O eixo OX é denominado eixo das abscissas e o eixo OY é denominado eixo das ordenadas.
O ponto O(0,0) é a origem do sistema de coordenadas cartesianas.
Os sinais algébricos de a e b definem regiões do plano denominadas QUADRANTES.
No 1º quadrante, a e b são positivos, no 2º quadrante, a é negativo e b positivo, no 3º quadrante, ambos são negativos e finalmente no 4º quadrante a é positivo e b negativo.
Observe que todos os pontos do eixo OX tem ordenada nula e todos os pontos do eixo OY tem abscissa nula. Assim, dizemos que a equação do eixo OX é y = 0 e a equação do eixo OY é
x = 0.
Os pontos do plano onde a = b, definem uma reta denominada bissetriz do 1º quadrante, cuja equação evidentemente é y = x.
Já os pontos do plano onde a = -b (ou b = - a), ou seja, de coordenadas simétricas, definem uma reta denominada bissetriz do 2º quadrante, cuja equação evidentemente é y = - x.
Os eixos OX e OY são denominados eixos coordenados.
EXERCICIO DE FIXAÇÃO
a) m é um número primo
b) m é primo e par
c) m é um quadrado perfeito
d) m = 0
e) m < 4
2) Se o ponto P(r - 12 , 4r - 6) pertença à primeira bissetriz , então podemos afirmar que :
a) r é um número natural
b) r = - 3
c) r é raiz da equação x3 - x2 + x + 14 = 0
d) r é um número inteiro menor do que - 3 .
e) não existe r nestas condições .
3) Se o ponto P(k , -2) satisfaz à relação x + 2y - 10 = 0 , então o valor de k 2 é :
a) 200
b) 196
c) 144
d) 36
e) 0
2 - Fórmula da distância entre dois pontos do plano cartesiano
Dados dois pontos do plano A(Xa,Ya) e B(Xb,Yb) , deduz-se facilmente usando o teorema de Pitágoras a seguinte fórmula da distancia entre os pontos A e B:
Dados dois pontos do plano A(Xa,Ya) e B(Xb,Yb) , deduz-se facilmente usando o teorema de Pitágoras a seguinte fórmula da distancia entre os pontos A e B:
Esta fórmula também pode ser escrita como: d2AB = (Xb - Xa)2 + (Yb - Ya)2 , obtida da anterior, elevando-se ao quadrado (quadrando-se) ambos os membros.
EXERCÍCIO DE FIXAÇÃO
a) (3,0)
b) (0, -1)
c) (0,4)
d) (0,5)
e) (0, 3)
3 - Ponto médio de um segmento
Dado o segmento de reta AB , o ponto médio de AB é o ponto M Î AB tal que AM = BM .
Nestas condições, dados os pontos A(x1 , y1) e B(x2 , y2) , as coordenadas do ponto médio
M(xm , ym) serão dadas por:
EXERCÍCIO DE FIXAÇÃO
Sendo W o comprimento da mediana relativa ao lado BC do triângulo ABC onde A(0,0), B(4,6) e C(2,4) , então W2 é igual a:a) 25
b) 32
c) 34
d) 44
e) 16
LEIA COM ATENÇÃO O ASSUNTO Á SEGUIR; POIS IREMOS VER NAS PROXIMAS AULAS. QUALQUER DÚVIDA PODE SER TIRADA NO MSN OU NO FACEBOK:silvia-nery@live.com NOS HORÁRIOS TERÇAS DE 14:00 ás 16:00 3ºRO1 - RO2 APARTI DAS 16:30 ÁS 18:30
4 - Baricentro de um triângulo
Sabemos da Geometria plana , que o baricentro de um triângulo ABC é o ponto de encontro das 3 medianas . Sendo G o baricentro , temos que AG = 2 . GM onde M é o ponto médio do lado oposto ao vértice A (AM é uma das 3 medianas do triângulo).
Nestas condições , as coordenadas do baricentro G(xg , yg) do triângulo ABC onde A(xa , ya) , B(xb , yb) e C(xc , yc) é dado por :
Conclui-se pois que as coordenadas do baricentro do triângulo ABC, são iguais às médias aritméticas das coordenadas dos pontos A , B e C.
Assim, por exemplo, o baricentro (também conhecido como centro de gravidade) do triângulo ABC onde A(3,5) , B(4, -1) e C(11, 8) será o ponto G(6, 4). Verifique com o uso direto das fórmulas.
Exercício resolvido
Conhecendo-se o baricentro B(3,5), do triângulo XYZ onde X(2,5) , Y(-4,6) , qual o comprimento do segmento BZ?
Solução:Seja o ponto Z(a,b). Temos, pela fórmula do baricentro:
3 = (2 - 4 + a) / 3 e 5 = (5 + 6 + b) / 3
Daí, vem que a = 11 e b = 4. O ponto Z será portanto Z(11, 4).
Usando a fórmula da distância entre dois pontos, lembrando que B(3,5) e Z(11,4),
encontraremos BZ = 651/2 u.c. (u.c. = unidades de comprimento).
Agora resolva este:
Os pontos A(m, 7), B(0, n) e C(3, 1) são os vértices de um triângulo cujo baricentro é o ponto
G(6, 11). Calcule o valor de m2 + n2.
Resposta: 850
Nenhum comentário:
Postar um comentário